文章:蔡健發 Andrew Choi Kin Fat (24 Oct 2025)
備注:本文未經過精密科學驗證,偏向哲學科學理論思想。
引言:宇宙是否由因果編織?
你有沒有想過,宇宙中的一切——從星星的閃爍到手機的運作——是否都源自一連串的因果關係?從牛頓的蘋果落地到愛因斯坦的相對論,科學家用數學描繪了宇宙的規律,這些規律似乎都指向一個簡單的真理:每件事都是一個「因」導致一個「果」(Hume, 1748/2007)。但當我們深入量子力學的世界,事情變得不再那麼簡單。量子不確定性——那種讓粒子行為捉摸不定的神秘現象——似乎挑戰了傳統的因果觀念,甚至讓我們質疑數學是否真的能揭示宇宙的全部真相(Heisenberg, 1927)。
在這篇文章中,我將分享一個猜想:宇宙中的一切是因果的結果,數學可能是人類基於因果經驗創造的工具,因此可能無法完全描述真實世界。更進一步,我認為量子力學中的不確定性可能不只是一個現象,而是一個「因」,在因果鏈中扮演關鍵角色。讓我們一起探索這個想法,看看它如何解釋量子世界的神秘,並揭示數學的局限性。
因果論:宇宙的編織者?
我的猜想始於一個簡單的觀點:宇宙中的一切——無論是行星的運動、水的流動,還是你此刻閱讀這篇文章——都是因果關係的結果。牛頓力學告訴我們,力(因)導致加速度(果),這可以用數學公式 F=ma 精確描述(Newton, 1687/1999)。化學也揭示了因果機制,例如氫和氧結合(因)形成水分子(果)(Pauling, 1960)。
但問題來了:如果一切都是因果的結果,那麼因果鏈的起點是什麼?是大爆炸?還是某種更基礎的東西?更重要的是,數學——這個我們用來描述因果關係的工具——是否真的能捕捉宇宙的全部真相?我猜想,數學可能不是宇宙的「內建語言」,而是人類基於因果經驗建構的工具(Wigner, 1960)。如果真是這樣,數學可能有其局限性,尤其是在面對量子力學的怪現象時。
量子不確定性:規則的破壞者還是因果的起點?
量子力學是現代物理學的奇妙領域,它揭示了微觀世界的奇怪規律。其中最著名的就是不確定性原理,由海森堡提出,告訴我們無法同時精確測量粒子的位置和動量(Heisenberg, 1927)。數學上,這可以用公式表示:
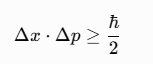
這意味著,如果你知道一個粒子的位置越精確,它的動量就越不確定,反之亦然(Feynman, Leighton, & Sands, 1964)。這與我們熟悉的經典世界完全不同:在牛頓的世界裡,給定初始條件,我們可以預測一切;但在量子世界,概率取代了確定性。
這種不確定性讓我思考:它是否只是宇宙的「限制」,還是某種更深層的東西?我提出一個大膽的想法:量子不確定性可能是一個「因」,驅動後續的物理現象。例如,在雙縫實驗中,電子通過狹縫時的不確定性(位置和動量的概率分佈)決定了干涉圖案的形成(Feynman et al., 1964)。又如,波函數坍縮(從疊加態到確定態)可能是一個「因」,影響後續的粒子行為(Bohr, 1928)。如果不確定性真的是一個「因」,這意味著量子世界的因果關係與經典世界不同。它不是簡單的「力導致運動」,而是一種概率性的因果,可能以不確定性為起點,引發一連串的結果(Reichenbach, 1956)。
數學:宇宙的語言還是人類的工具?
數學是科學的語言,從牛頓的引力公式到愛因斯坦的
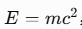
它幫助我們理解宇宙的規律(Einstein, 1915/2005)。但我開始懷疑:數學真的是宇宙的「真理」,還是人類基於因果經驗創造的工具?想想數學的歷史:幾何學起源於測量土地,代數來自解決商業問題,概率論誕生於賭博遊戲(Hacking, 1975)。這些數學分支都根植於人類對因果現象的觀察。如果數學是因果的產物,它可能更擅長描述經典世界的確定性規律(例如行星軌道),但在量子世界的不確定性面前,它可能顯得力不從心。
例如,量子力學用波函數描述粒子的概率分佈,但無法解釋波函數為什麼會坍縮(即測量問題)(Bohr, 1928)。這是否意味著數學有其局限性?如果不確定性是一個「因」,而數學無法完全捕捉它的機制,這是否表明數學無法揭示宇宙的全部真相?我的猜想是,數學作為因果經驗的產物,可能無法完全描述量子世界的真實結構(Wigner, 1960)。
不確定性與數學的局限性
量子不確定性為我的猜想提供了一個完美的測試場景。以下是幾個支持我的想法的觀點:
- 數學的因果根源:數學的發展依賴於人類對經典世界的觀察(例如牛頓力學的確定性)。在量子世界,不確定性作為一個「因」可能超越了傳統數學的描述能力。例如,波函數坍縮的過程至今沒有完整的數學模型,這可能反映數學的局限性(Bohr, 1928)。
- 新的因果框架:如果不確定性是一個「因」,這可能需要一種新的數學框架來描述概率性因果。例如,現有的概率論可以預測量子事件的統計規律,但無法解釋不確定性的本質(Reichenbach, 1956)。
- 隱變量還是本質不確定性?:一些物理學家(如愛因斯坦)認為不確定性只是表象,背後有隱藏的因果機制(隱變量理論)(Einstein, Podolsky, & Rosen, 1935)。如果這正確,我的因果論得到支持;但如果不確定性是本質的(如哥本哈根詮釋),這可能意味著宇宙的真實結構超越了數學的描述範圍(Bohr, 1928)。
探索未來的可能性
我的猜想——宇宙中的一切是因果的結果,數學可能是因果的產物,量子不確定性可能是一個「因」——開啟了許多值得探索的問題:
- 數學能否進化? 如果數學無法完全描述不確定性,我們是否需要新的數學框架,例如超越概率論的工具?(Penrose, 1989)
- 不確定性是否隱藏更深的因果? 隱變量理論或弦論是否能揭示不確定性背後的因果機制?(Bohm, 1952)
- 宇宙的真實結構是什麼? 如果數學有局限性,宇宙的「真實」是否超越了我們當前的理解?(Wigner, 1960)
這些問題需要更多的研究,可能通過模擬量子現象(例如雙縫實驗)、分析實驗數據(例如量子糾纏測試),或從哲學角度重新思考因果和數學的本質。
結論:量子不確定性與宇宙的謎團
量子力學的不確定性不僅僅是一個科學難題,它可能是解開宇宙因果結構和數學本質的鑰匙。我的猜想提出,宇宙中的一切是因果的結果,數學可能是人類基於因果經驗創造的工具,而不確定性可能是一個驅動量子現象的「因」。如果這正確,數學的局限性可能在量子世界中顯露無遺,因為它無法完全捕捉不確定性作為因果機制的複雜性(Bohr, 1928; Wigner, 1960)。
這個猜想不僅挑戰了我們對因果的傳統理解,也讓我們重新思考數學的角色。或許,宇宙的真實結構比我們想像的更深邃,而不確定性正是通往這一真相的線索。你認為呢?量子不確定性是宇宙的限制,還是因果鏈的起點?
參考文獻
Bohm, D. (1952). A suggested interpretation of the quantum theory in terms of “hidden” variables. Physical Review, 85(2), 166–193. https://doi.org/10.1103/PhysRev.85.166
Bohr, N. (1928). The quantum postulate and the recent development of atomic theory. Nature, 121(3050), 580–590. https://doi.org/10.1038/121580a0
Einstein, A. (2005). Relativity: The special and general theory (R. W. Lawson, Trans.). Penguin Classics. (Original work published 1915)
Einstein, A., Podolsky, B., & Rosen, N. (1935). Can quantum-mechanical description of physical reality be considered complete? Physical Review, 47(10), 777–780. https://doi.org/10.1103/PhysRev.47.777
Feynman, R. P., Leighton, R. B., & Sands, M. (1964). The Feynman lectures on physics, Vol. III: Quantum mechanics. Addison-Wesley.
Hacking, I. (1975). The emergence of probability: A philosophical study of early ideas about probability, induction and statistical inference. Cambridge University Press.
Heisenberg, W. (1927). Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Zeitschrift für Physik, 43(3–4), 172–198. https://doi.org/10.1007/BF01397280
Hume, D. (2007). An enquiry concerning human understanding (P. Millican, Ed.). Oxford University Press. (Original work published 1748)
Newton, I. (1999). Mathematical principles of natural philosophy (I. B. Cohen & A. Whitman, Trans.). University of California Press. (Original work published 1687)
Pauling, L. (1960). The nature of the chemical bond and the structure of molecules and crystals: An introduction to modern structural chemistry (3rd ed.). Cornell University Press.
Penrose, R. (1989). The emperor’s new mind: Concerning computers, minds, and the laws of physics. Oxford University Press.
Reichenbach, H. (1956). The direction of time. University of California Press.
Wigner, E. P. (1960). The unreasonable effectiveness of mathematics in the natural sciences. Communications on Pure and Applied Mathematics, 13(1), 1–14. https://doi.org/10.1002/cpa.3160130102